decider for offchain verification

Overview: This section describes the Decider (compressed SNARK / final proof) for the non-ethereum use cases in which the verification of the Nova+CycleFold proofs is done offchain. For onchain Ethereum use cases, check out the decider-onchain section.

Setup

At the final stage of the Nova+CycleFold folding, after $d$ iterations, we have the committed instances ${u_{d}, U_{d}, U_{EC, d}}$ and their respective witnessess.

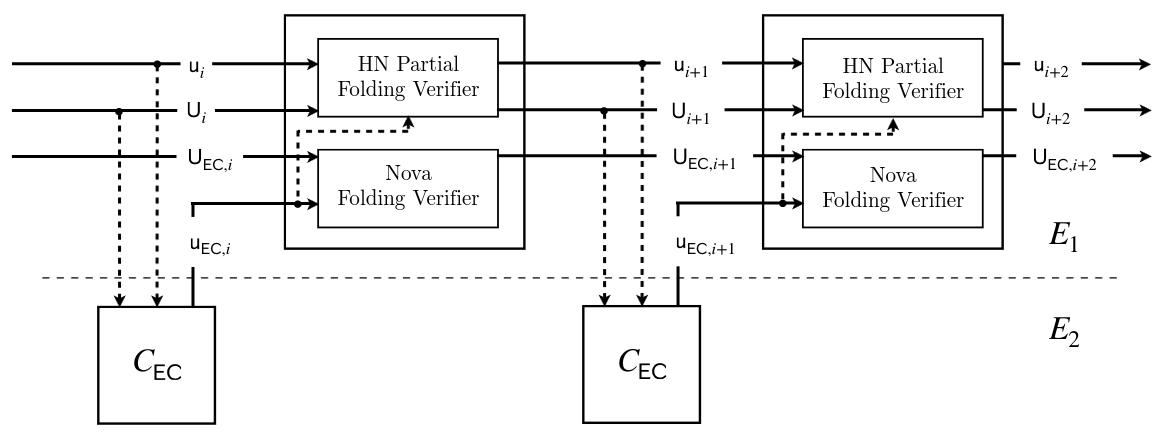cyclefold diagram Diagram source: CycleFold paper (https://eprint.iacr.org/2023/1192.pdf). In the case of this document $d = i + 2$ , so $u_{i + 2} = u_{d}$ , $U_{i + 2} = U_{d}$ , $U_{EC, i + 2} = U_{EC, d}$ .

We work with a cycle of curves $E_{1}$ and $E_{2}$ , where $E_{1} . F_{r} = E_{2} . F_{q}$ and $E_{1} . F_{q} = E_{2} . F_{r}$ . We will use $F_{r}$ for referring to $E_{1} . F_{r} = E_{2} . F_{q}$ , and $F_{q}$ for referring to $E_{1} . F_{q} = E_{2} . F_{r}$ . The main circuit constraint field is $F_{r}$ , and $C_{EC}$ circuit constraint field is $F_{q}$ .

The $u_{d}$ and $U_{d}$ contain: ${\overline{E} \in E_{1}, \overline{W} \in E_{1}, u \in F_{r}, x \in F_{r}}$

And $U_{EC, d}$ contains: ${\overline{E} \in E_{2}, \overline{W} \in E_{2}, u \in F_{q}, x \in F_{q}^{n}}$

Decider high level checks

$U_{n + 1}$ is the correct folding of $U_{n}, u_{n}$ , i.e., $N I FS . V (r, U_{n}, u_{n}, \overline{T}) = U_{n + 1}$ .
$R_{r 1 cs} (W_{n + 1}, U_{n + 1}) = 1$ :
- The running instance $U_{n + 1}$ and witness $W_{n + 1}$ satisfy (relaxed) $r 1 cs$ .
- The commitments in $U_{n + 1}$ (i.e., $U_{n + 1} . {\overline{E}, \overline{W}} \in E_{1}$ ) open to the values in $W_{n + 1}$ (i.e., $W_{n + 1} . {E, W}$ ).
$R_{r 1 c s_{EC}} (W_{EC, n}, U_{EC, n})$ :
- The CycleFold instance $U_{EC, n}$ and witness $W_{EC, n}$ satisfy (relaxed) $r 1 c s_{EC}$ .
- The commitments in $U_{EC, n}$ (i.e., $U_{EC, n} . {\overline{E}, \overline{W}} \in E_{2}$ ) open to the values in $W_{EC, n}$ (i.e., $W_{EC, n} . {E, W}$ ).
$u_{n}$ is valid:
- $u_{n} . x$ contains the correct hash of the initial and final states, i.e., $u_{n} . x_{0} = H (n, z_{0}, z_{n}, U_{n})$ and $u_{n} . x_{1} = H (U_{EC, n})$
- $u_{n}$ is indeed an incoming instance, i.e., $u_{n} . \overline{E} = 0$ and $u_{n} . u = 1$ .

Note: These are the same checks for both the Onchain & Offchain Deciders. The difference lays on how are performed.

Offchain Decider approach

In the offchain case, since we can end up with proofs in both curves of the cycle, we try to fit all the computations natively in each curve respectively.

We use the same checks numbers as the ones used in the Onchain Decider in order to make the relation of the checks easier to follow.

Circuit1 $\in F r$ ( $E_{1} . F_{r}$ )

1: Enforce $U_{n + 1}$ and $W_{n + 1}$ satisfy $r 1 cs$ , the RelaxedR1CS relation of the AugmentedFCircuit
2: Check that $u_{n} . \overline{E} = 0$ and $u_{n} . u = 1$
3: Check that $u_{n} . x_{0} = H (n, z_{0}, z_{n}, U_{n})$ and $u_{n} . x_{1} = H (U_{EC, n})$
6.1: Partially enforce that $U_{n + 1}$ is the correct folding of $U_{n}, u_{n}$
- By partially, we mean that only field elements in $U_{n + 1}$ are checked, while the group elements (i.e., commitments) are not, as they are in $E_{1}$ and are expensive non-native operations.
7.1: Check correct computation of the KZG challenges $c_{E} = H (\overline{E} . {x, y}), c_{W} = H (\overline{W} . {x, y})$ which we do through in-circuit Transcript.
7.2: Check that the KZG evaluations are correct
- $e v a l_{W} == p_{W} (c_{W})$
- $e v a l_{E} == p_{E} (c_{E})$
  where $p_{W}, p_{E} \in F [X]$ are the interpolated polynomials from $W_{i + 1} . W, W_{i + 1} . E$ respectively.
  ie. $p_{W} (x) = in t er p o l a t e (W_{i + 1} . W, 0)$ , where $0$ is zero-padding to the next power of 2 length, and $in t er p o l a t e ()$ interpolates a (unique) polynomial from the vector

Circuit2 $\in Fq$ ( $E_{2} . F_{r}$ )

Note that in onchain decider, step 4 (Pedersen commitments verification of $U_{EC, n} . {\overline{E}, \overline{W}}$ ) is checked in-circuit, necessitating ~5M constraints.

In the case of offchain decider, we aim to reduce the number of constraints for commitment verification for CycleFold instances. To this end, we apply the same approach as in step 7 of the onchain decider for checking commitments in primary instances. That is, we now use KZG commitments as well for the CycleFold instances, enabling us to separate expensive parts in commitments verification from the circuit.

Below are checks for the Circuit2:

4.1: Check correct computation of the KZG challenges for $U_{EC}$ $c_{E} = H (U_{EC} . \overline{E} . {x, y}), c_{W} = H (U_{EC} . \overline{W} . {x, y})$ which we do through in-circuit Transcript.
4.2: check that the KZG evaluations for $U_{EC}$ are correct
- $e v a l_{W} == p_{W} (c_{W})$
- $e v a l_{E} == p_{E} (c_{E})$
  where $p_{W}, p_{E} \in F [X]$ are the interpolated polynomials from $W_{i + 1} . W, W_{i + 1} . E$ respectively.
5: Enforce $U_{EC, n}$ and $W_{EC, n}$ satisfy $r 1 c s_{EC}$ , the RelaxedR1CS relation of the CycleFoldCircuit
- This check becomes native because the constraint system is now over $F_{q}$ .

Outside the circuits

6.2. Check the commitments in $U_{n + 1}$ are the correct folding of those in $U_{n}, u_{n}$
7.3: Verify the KZG proofs with respect to the commitments $U_{n + 1} . {\overline{E}, \overline{W}} \in E_{1}$ and the challenges $c_{E}, c_{W}$ .
4.3: Verify the KZG proofs with respect to the commitments $U_{EC, n} . {\overline{E}, \overline{W}} \in E_{2}$ and the challenges $c_{E}, c_{W}$ .

Proving scheme

We could use a SNARK adapted to RelaxedR1CS, but before that is ready we use a regular R1CS SNARK and check the RelaxedR1CS relations in-circuit as described above. Two proofs are generated, one for each circuit over their respective curves of the cycle.

sonobe docs