Decider for Onchain Verification

Overview

This section describes the details of Sonobe's Decider, which is a zkSNARK that compresses the IVC's final proof.

Given an IVC scheme constructed with a folding scheme based on the CycleFold approach, the decider described in this section allows one to efficiently verify the final proof onchain in Ethereum's EVM.

Below we use Nova as a concrete example of the folding scheme, but the decider itself is generic and can be used with any other folding scheme.

Warning: This section, as the rest of Sonobe, is experimental. The approach described in this section is highly experimental and has not been audited.

Context

At the final stage of IVC based on Nova+CycleFold, after $n$ iterations, we have the committed instances $\{u_n,U_n,U_{EC,n}\}$ and their respective witnessess, where $u_n$ is the incoming instance, $U_n$ is the running instance, and $U_{EC,n}$ is the CycleFold (running) instance.

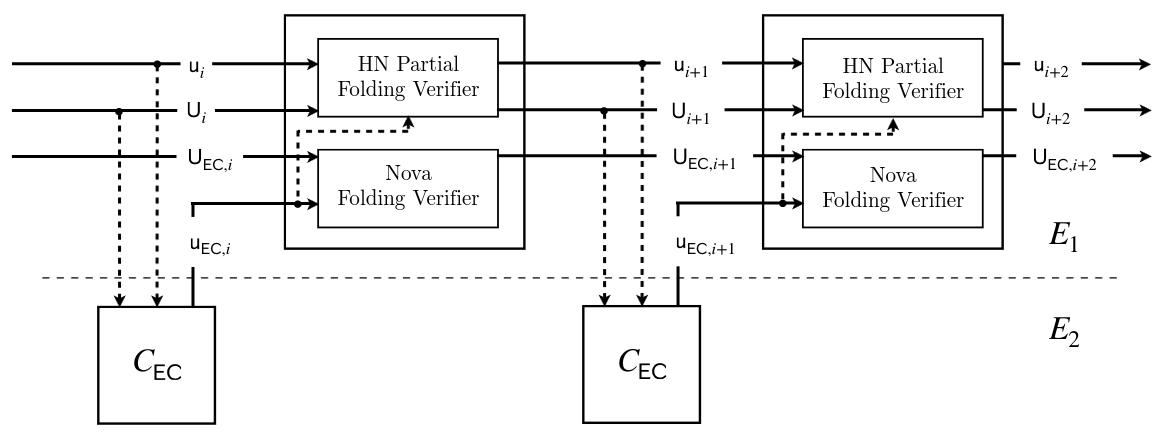Diagram source: CycleFold paper (https://eprint.iacr.org/2023/1192.pdf). In the case of this document $n=i+2$, so $u_{i+2}=u_n$, $U_{i+2}=U_n$, $U_{EC,i+2}=U_{EC,n}$.

We work on a cycle of curves composed by $E_1$ and $E_2$, where $E_1.F_r=E_2.F_q$ and $E_1.F_q=E_2.F_r$. We will use $F_r$ to refer to $E_1.F_r=E_2.F_q$, and $F_q$ to refer to $E_1.F_q=E_2.F_r$. The main circuit constraint field is $F_r$, and $C_{EC}$ circuit constraint field is $F_q$.

Since the objective is to verify the proofs on Ethereum, we set $E_1$=BN254 and $E_2$=Grumpkin. Thus, $F_r$ is the scalar field of the BN254.

The $u_n$ and $U_n$ contain: $\{\overline{E}\in E_1,\overline{W}\in E_1,u\in F_r,x\in F_r^{|io|}\}$

And $U_{EC,n}$ contains: $\{\overline{E}\in E_2,\overline{W}\in E_2,u\in F_q,x\in F_q^{|io|}\}$

Decider high level checks

Consider the Nova-based IVC for R1CS, where $r1cs$ is the R1CS for the augmented circuit AugmentedFCircuit, and $r1c{s}_{EC}$ is the R1CS for the CycleFold circuit CycleFoldCircuit.

The decider is essentially responsible for ensuring the validity of $IVC.V$, which contains the following checks:

• $R_{r1cs}(W_n,U_n)=1$:
  • The running instance $U_n$ and witness $W_n$ satisfy (relaxed) $r1cs$.
  • The commitments in $U_n$ open to the values in $W_n$.
• $R_{r1cs}(w_n,u_n)=1$:
  • The incoming instance $u_n$ and witness $w_n$ satisfy (plain) $r1cs$.
  • The commitments in $u_n$ open to the values in $w_n$.
• $R_{r1c{s}_{EC}}(W_{EC,n},U_{EC,n})$:
  • The CycleFold instance $U_{EC,n}$ and witness $W_{EC,n}$ satisfy (relaxed) $r1c{s}_{EC}$.
  • The commitments in $U_{EC,n}$ open to the values in $W_{EC,n}$.
• $u_n$ is valid:
  • $u_n.x$ contains the correct hash of the initial and final states.
  • $u_n$ is indeed an incoming instance.

In Sonobe, the logic above is implemented in a zkSNARK circuit. To reduce circuit size, we ask the prover to fold $W_n,U_n$ and $w_n,u_n$ one more time, obtaining $W_{n+1},U_{n+1}$. Now, the circuit only needs to check:

• $U_{n+1}$ is the correct folding of $U_n,u_n$, i.e., $NIFS.V(r,U_n,u_n,\overline{T})=U_{n+1}$.
• $R_{r1cs}(W_{n+1},U_{n+1})=1$:
  • The running instance $U_{n+1}$ and witness $W_{n+1}$ satisfy (relaxed) $r1cs$.
  • The commitments in $U_{n+1}$ (i.e., $U_{n+1}.\{\overline{E},\overline{W}\}\in E_1$) open to the values in $W_{n+1}$ (i.e., $W_{n+1}.\{E,W\}$).
• $R_{r1c{s}_{EC}}(W_{EC,n},U_{EC,n})$:
  • The CycleFold instance $U_{EC,n}$ and witness $W_{EC,n}$ satisfy (relaxed) $r1c{s}_{EC}$.
  • The commitments in $U_{EC,n}$ (i.e., $U_{EC,n}.\{\overline{E},\overline{W}\}\in E_2$) open to the values in $W_{EC,n}$ (i.e., $W_{EC,n}.\{E,W\}$).
• $u_n$ is valid:
  • $u_n.x$ contains the correct hash of the initial and final states, i.e., $u_n.x_0=H(n,z_0,z_n,U_n)$ and $u_n.x_1=H(U_{EC,n})$
  • $u_n$ is indeed an incoming instance, i.e., $u_n.\overline{E}=0$ and $u_n.u=1$.

Note: These are the same checks for both the Onchain & Offchain Deciders. The difference lays on how are performed.

Onchain Decider approach

The decider proof is computed once, and after all the folding has taken place. Our aim is to be able to verify this proof in the Ethereum's EVM.

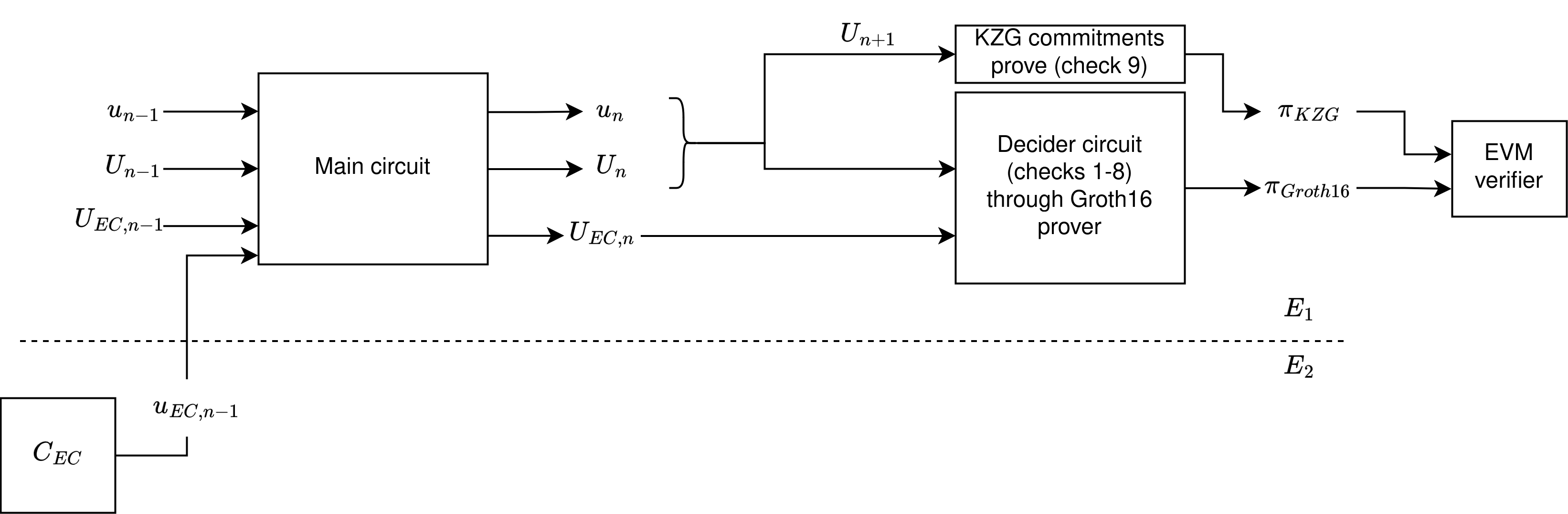
The prover computes $(U_{n+1},W_{n+1},\overline{T})=NIFS.P((U_n,W_n),(u_n,w_n))$

The Decider Circuit verifies in its R1CS relation over $F_r$ the checks described above. Below we explain how the checks are performed in the circuit (for circuit efficiency, the order of the checks is different from the one described above):

• 1: Enforce $U_{n+1}$ and $W_{n+1}$ satisfy $r1cs$, the RelaxedR1CS relation of the AugmentedFCircuit
• 2: Check that $u_n.\overline{E}=0$ and $u_n.u=1$
• 3: Check that $u_n.x_0=H(n,z_0,z_n,U_n)$ and $u_n.x_1=H(U_{EC,n})$
• 4: Commitments verification of $U_{EC,n}.\{\overline{E},\overline{W}\}$ with respect to $W_{EC,n}.\{E,W\}$, where Pedersen commitments are used
  • This check is native in $F_r$ because $U_{EC,n}.\{\overline{E},\overline{W}\}\in E_2$.
• 5: Enforce $U_{EC,n}$ and $W_{EC,n}$ satisfy $r1c{s}_{EC}$, the RelaxedR1CS relation of the CycleFoldCircuit
  • This check involves non-native operations because $W_{EC,n}.\{E,W\}\in F_q$. With naive sparse matrix-vector product, it blows up the number of constraints.
• 6.1: Partially enforce that $U_{n+1}$ is the correct folding of $U_n,u_n$
  • By partially, we mean that only field elements in $U_{n+1}$ are checked, while the group elements (i.e., commitments) are not, as they are in $E_1$ and are expensive non-native operations.
• 7.1: Check correct computation of the KZG challenges $$c_E=H(\overline{E}.\{x,y\}),c_W=H(\overline{W}.\{x,y\})$$ which we do through in-circuit Transcript.
• 7.2: Check that the KZG evaluations are correct
  • $eva{l}_W==p_W(c_W)$
  • $eva{l}_E==p_E(c_E)$
    where $p_W,p_E\in \mathbb{F}[X]$ are the interpolated polynomials from $W_{i+1}.W,W_{i+1}.E$ respectively.
    ie. $p_W(x)=interpolate(W_{i+1}.W,0)$, where $0$ is zero-padding to the next power of 2 length, and $interpolate()$ interpolates a (unique) polynomial from the vector

The rest of the checks are performed outside of the circuit by the verifier. In addition to verifying the decider proof, the verifier would have to check:

• 6.2: The commitments in $U_{n+1}$ are the correct folding of those in $U_n,u_n$, i.e., $U_{n+1}.\overline{E}=U_n.\overline{E}+r\cdot \overline{T}$ and $U_{n+1}.\overline{W}=U_n.\overline{W}+r\cdot u_n.\overline{W}$.
  • 6.1 and 6.2 in together enforce $NIFS.V(r,U_n,u_n,\overline{T})=U_{n+1}$.
• 7.3: The KZG proofs are valid with respect to the commitments $U_{n+1}.\{\overline{E},\overline{W}\}$ and the challenges $c_E,c_W$.
  • 7.1, 7.2, and 7.3 together enforce that $W_{n+1}.\{E,W\}$ are the openings to the commitments $U_{n+1}.\{\overline{E},\overline{W}\}$.

If we use Pedersen commitment as the commitment scheme for generating $U_{n+1}$, the checks for commitments would be too expensive as they are non-native in-circuit. By changing the commitment scheme to KZG, we can separate the commitments verification into 7.1, 7.2, and 7.3, where 7.1 and 7.2 can be (relatively) cheaply verified in-circuit, and 7.3 can be verified outside of the circuit (onchain).

The prover would generate a Groth16 proof over BN254 for this Decider Circuit, which can later be verified onchain in the EVM together with the KZG commitments of check 7.1 and check 7.2.

In this way, the final proof to be verified onchain would be:

• a Groth16 proof of the checks 1, 2, 3, 4, 5, 6.1, 7.1, 7.2
• the KZG proofs verification (check 7.3)
• the NIFS.V (check 6.2), which relates the inputs of the checks in the Groth16 proof and check 6.1

The RelaxedR1CS checker circuit

The "correct RelaxedR1CS relation" (used in check 1) is checked by the gadget proposed by Nalin Bhardwaj, which is a R1CS circuit that checks the RelaxedR1CS relation, more details here.

The idea is that we check in a R1CS circiut the RelaxedR1CS relation ($Az\circ Bz-uCz-E=0$). Note that this approach has a blowup of 3x with respect to the original circuit number of constraints x (when using sparse representation of the matrices).

Circuit costs

Note: the number of constraints written in this section is the current values that we have, which we aim to reduce in future iterations.

Estimated costs of the full decider-onchain circuit:

(x is the number of constraints of the circuit that we're folding, and the AugmentedFCircuit takes ~52k constraints)

• 1: $U_{n+1}$ relation: 3(x+52k)
• 2: $u_n$ check: <1000
• 3: $u_n.x$ hash check: 2634
• 4: Pedersen check of $U_{EC,n}$ commitments (native): <5M both commitments (including the inputs allocations). This is a couple of native MSMs of <1500 elements each one
• 5: $U_{EC,n}$ relation (non-native): 5.1M
• 6.1: Partial check of $NIFS.V$: (cheap)
• 7.1: Check correct computation of the KZG challenges: 7708
• 7.2: Check that the KZG evaluations are correct 262k

Total: 3*(x+52_252) + 1000 + 2634 + 4_967_155 + 5_146_236 + 7708 + 262_000

eg: for a circuit of 500k constraints the decider circuit would take approximately 11.9M constraints.

As can be seen, most of the costs come from the Pedersen commitments verification and the $U_{EC,n}$ relation (checks 4 and 5 respectively).