Folding schemes and Sonobe

Folding schemes overview

Folding schemes efficiently achieve incrementally verifiable computation (IVC), where the prover recursively proves the correct execution of the incremental computations. Once the IVC iterations are completed, the IVC proof is compressed into the Decider proof, a zkSNARK proof which proves that applying $n$ times the $F$ function (the circuit being folded) to the initial state ($z_0$) results in the final state ($z_n$).

Where $w_i$ are the external witnesses used at each iterative step.

In other words, it allows to prove efficiently that $z_n=F(...F(F(F(F(z_0,w_0),w_1),w_2),...),w_{n-1})$.

The next 3 videos provide a good overview of folding schemes:

• In this presentation (5 min) Abhiram Kothapalli explains the main idea of Nova folding scheme.
• In this presentation (20 min) Carlos Pérez overviews the features of folding schemes and what can be built with them.
• In this presentation (1h) Justin Drake explains what a folding scheme is and Nova-related concepts.

Sonobe overview

Sonobe is a folding schemes modular library to fold arithmetic circuit instances in an incremental verifiable computation (IVC) style. It also provides the tools required to generate a zkSNARK proof out of an IVC proof and to verify it on Ethereum's EVM.

The development flow using Sonobe looks like:

1. Define a circuit to be folded
2. Set which folding scheme to be used (eg. Nova with CycleFold)
3. Set a final decider to generate the final proof (eg. Spartan over Pasta curves)
4. Generate the the decider verifier

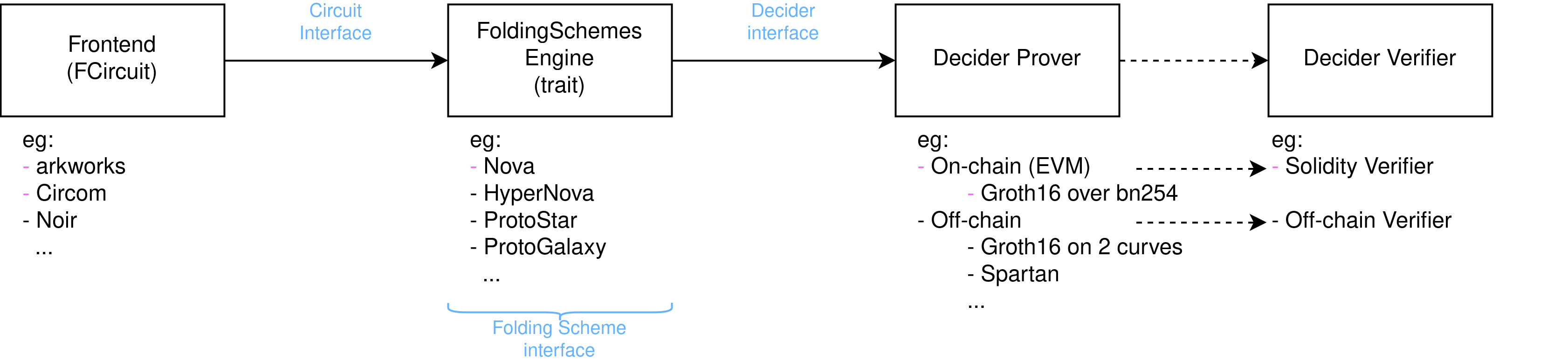
The folding scheme and decider used can be swapped respectively with a few lines of code (eg. switching from a Decider that uses two Spartan proofs over a cycle of curves, to a Decider that uses a single Groth16 proof over the BN254 to be verified in an Ethereum smart contract).

Complete examples can be found at sonobe/folding-schemes/examples.