sonobe

Experimental folding schemes library implemented in a joint effort by 0xPARC and PSE.

https://github.com/privacy-scaling-explorations/sonobe

Sonobe is a modular library to fold circuit instances in an Incremental Verifiable computation (IVC) style. It features multiple folding schemes and decider setups, allowing users to pick the scheme which best fit their needs.

Sonobe is conceived as an exploratory effort with the aim to push forward the practical side of folding schemes and advancing towards onchain (EVM) verification.

"The Sonobe module is one of the many units used to build modular origami. The popularity of Sonobe modular origami models derives from the simplicity of folding the modules, the sturdy and easy assembly, and the flexibility of the system."

Warning: experimental code, do not use in production.
The code has not been audited. Several optimizations are also pending. Our focus so far has been on implementing the Nova and CycleFold schemes and achieving onchain (EVM) verification.

Schemes implemented

The library uses arkworks, and implements the following folding schemes:

Nova: Recursive Zero-Knowledge Arguments from Folding Schemes, Abhiram Kothapalli, Srinath Setty, Ioanna Tzialla. 2021
CycleFold: Folding-scheme-based recursive arguments over a cycle of elliptic curves, Abhiram Kothapalli, Srinath Setty. 2023

Work in progress:

HyperNova: Recursive arguments for customizable constraint systems, Abhiram Kothapalli, Srinath Setty. 2023
ProtoGalaxy: Efficient ProtoStar-style folding of multiple instances, Liam Eagen, Ariel Gabizon. 2023

Available frontends

Available frontends to define the folded circuit:

arkworks, arkworks contributors
Circom, iden3, 0Kims Association. Experimental frontend using arkworks/circom-compat.

Folding schemes and Sonobe

Folding schemes overview

Folding schemes efficiently achieve incrementally verifiable computation (IVC), where the prover recursively proves the correct execution of the incremental computations. Once the IVC iterations are completed, the IVC proof is compressed into the Decider proof, a zkSNARK proof which proves that applying $n$ times the $F$ function (the circuit being folded) to the initial state ( $z_{0}$ ) results in the final state ( $z_{n}$ ).

Where $w_{i}$ are the external witnesses used at each iterative step.

In other words, it allows to prove efficiently that $z_{n} = F (... F (F (F (F (z_{0}, w_{0}), w_{1}), w_{2}), ...), w_{n - 1})$ .

The next 3 videos provide a good overview of folding schemes:

In this presentation (5 min) Abhiram Kothapalli explains the main idea of Nova folding scheme.
In this presentation (20 min) Carlos Pérez overviews the features of folding schemes and what can be built with them.
In this presentation (1h) Justin Drake explains what a folding scheme is and Nova-related concepts.

Sonobe overview

Sonobe is a folding schemes modular library to fold arithmetic circuit instances in an incremental verifiable computation (IVC) style. It also provides the tools required to generate a zkSNARK proof out of an IVC proof and to verify it on Ethereum's EVM.

The development flow using Sonobe looks like:

Define a circuit to be folded
Set which folding scheme to be used (eg. Nova with CycleFold)
Set a final decider to generate the final proof (eg. Spartan over Pasta curves)
Generate the the decider verifier

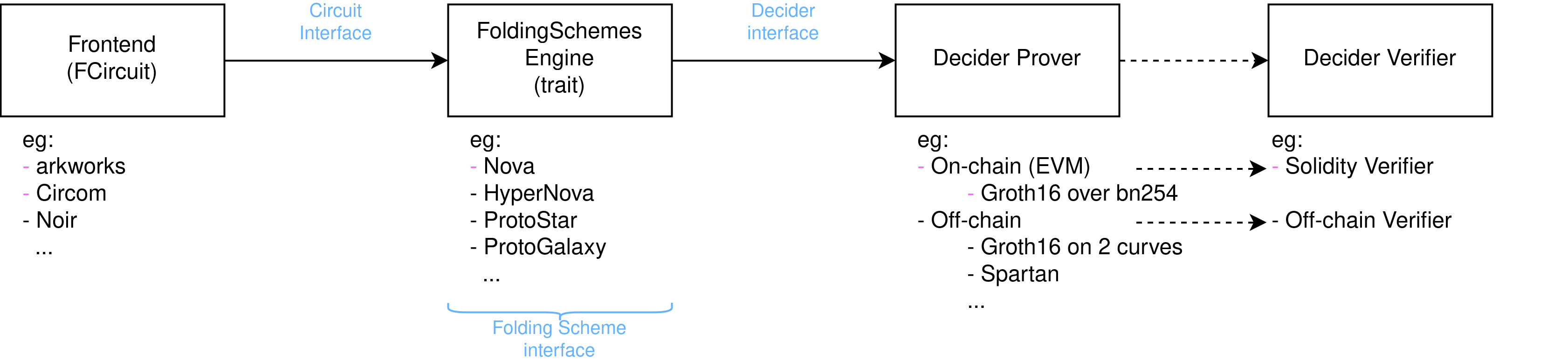
The folding scheme and decider used can be swapped respectively with a few lines of code (eg. switching from a Decider that uses two Spartan proofs over a cycle of curves, to a Decider that uses a single Groth16 proof over the BN254 to be verified in an Ethereum smart contract).

Complete examples can be found at sonobe/folding-schemes/examples.

Usage

This section showcases how to use the Sonobe library to:

Define a circuit to be folded using a frontend such as circom or arkworks.
Fold the circuit using one of the folding schemes
Generate a final Decider proof
Verify the Decider proof, and in Ethereum case, generate a Solidity verifier

Frontend

The frontend interface allows to define the circuit to be folded. The recommended frontend is to directly use arkworks to define the FCircuit, just following the FCircuit trait.

Alternatively, experimental frontends for Circom, Noir, and Noname can be found at sonobe/frontends, which have some computational (and time) overhead.

Defining a circuit to be folded is as simple as fulfilling the FCircuit trait interface. Henceforth, integrating a new zk circuits language into Sonobe, can be done by building a wrapper on top of it that satisfies the FCircuit trait.

The `FCircuit` trait

To be folded with sonobe, a circuit needs to implement the FCircuit trait. This trait defines the methods that sonobe expects from the circuit to be folded. It corresponds to the $F$ function that is being folded. The trait has the following methods:

#![allow(unused)]
fn main() {
/// FCircuit defines the trait of the circuit of the F function, which is the one being folded (ie.
/// inside the agmented F' function).
/// The parameter z_i denotes the current state, and z_{i+1} denotes the next state after applying
/// the step.
pub trait FCircuit<F: PrimeField>: Clone + Debug {
    type Params: Debug;

    /// returns a new FCircuit instance
    fn new(params: Self::Params) -> Result<Self, Error>;

    /// returns the number of elements in the state of the FCircuit, which corresponds to the
    /// FCircuit inputs.
    fn state_len(&self) -> usize;

    /// returns the number of elements in the external inputs used by the FCircuit. External inputs
    /// are optional, and in case no external inputs are used, this method should return 0.
    fn external_inputs_len(&self) -> usize;

    /// computes the next state values in place, assigning z_{i+1} into z_i, and computing the new
    /// z_{i+1}
    fn step_native(
        // this method uses self, so that each FCircuit implementation (and different frontends)
        // can hold a state if needed to store data to compute the next state.
        &self,
        i: usize,
        z_i: Vec<F>,
        external_inputs: Vec<F>, // inputs that are not part of the state
    ) -> Result<Vec<F>, Error>;

    /// generates the constraints for the step of F for the given z_i
    fn generate_step_constraints(
        // this method uses self, so that each FCircuit implementation (and different frontends)
        // can hold a state if needed to store data to generate the constraints.
        &self,
        cs: ConstraintSystemRef<F>,
        i: usize,
        z_i: Vec<FpVar<F>>,
        external_inputs: Vec<FpVar<F>>, // inputs that are not part of the state
    ) -> Result<Vec<FpVar<F>>, SynthesisError>;
}
}

Side note: adhoc frontend dependencies for the experimental frontends

Note: this affects only to the experimental frontends in the sonobe/frontends directory.

There are many ad hoc dependencies for each of the frontends integrated with Sonobe. Here are a few reasons why this is the case.

First, any frontend different from Arkworks needs a "bridge"—a way to "translate" constraints from one R1CS framework to another. Indeed, Sonobe uses Arkworks as its constraint writing framework under the hood. Therefore, any R1CS written with another framework (e.g., Circom) will need to port its constraint system to Arkworks.

Second, R1CS bridge libraries are often developed by teams assuming that public and private witness values will be assigned simultaneously. This is typically the standard approach. However, folding schemes differ, as they redirect the public outputs of one computation to the public inputs of the next step. This means that public inputs are already assigned when calling the "bridge" to port whatever frontend constraints to Sonobe.

Consequently, we had to make a few ad hoc changes to each of these bridges to make them compatible with Sonobe. We are aware that this significantly increases dependencies, which also raises maintenance requirements. The topic of how to reduce our reliance on such ad hoc changes in the future is being actively discussed.

Arkworks frontend

Let's walk through different simple examples implementing the FCircuit trait. By the end of this section, you will hopefully be familiar with how to integrate an arkworks circuit into sonobe.

You can find most of the following examples with the rest of code to run them at the examples directory of the Sonobe repo.

Cubic circuit example

This first example implements the FCircuit trait for the R1CS example circuit from Vitalik's post, which checks $x^{3} + x + 5 == y$ .

$z_{i}$ is used as $x$ , and $z_{i + 1}$ is used as $y$ , and at the next step, $z_{i + 1}$ will be assigned to $z_{i}$ , and a new $z_{i + 1}$ will be computted.

#![allow(unused)]
fn main() {
#[derive(Clone, Copy, Debug)]
pub struct CubicFCircuit<F: PrimeField> {
    _f: PhantomData<F>,
}
impl<F: PrimeField> FCircuit<F> for CubicFCircuit<F> {
    type Params = ();
    fn new(_params: Self::Params) -> Result<Self, Error> {
        Ok(Self { _f: PhantomData })
    }
    fn state_len(&self) -> usize {
        1
    }
    fn external_inputs_len(&self) -> usize {
        0
    }
    fn step_native(
        &self,
        _i: usize,
        z_i: Vec<F>,
        _external_inputs: Vec<F>,
    ) -> Result<Vec<F>, Error> {
        Ok(vec![z_i[0] * z_i[0] * z_i[0] + z_i[0] + F::from(5_u32)])
    }
    fn generate_step_constraints(
        &self,
        cs: ConstraintSystemRef<F>,
        _i: usize,
        z_i: Vec<FpVar<F>>,
        _external_inputs: Vec<FpVar<F>>,
    ) -> Result<Vec<FpVar<F>>, SynthesisError> {
        let five = FpVar::<F>::new_constant(cs.clone(), F::from(5u32))?;
        let z_i = z_i[0].clone();

        Ok(vec![&z_i * &z_i * &z_i + &z_i + &five])
    }
}
}

Multiple inputs circuit example

The following example has a state of 5 public elements. At each step, we will want the circuit to compute the next state by:

adding 4 to the first element
adding 40 to the second element
multiplying the third element by 4
multiplying the fourth element by 40
adding 100 to the fifth element

#![allow(unused)]
fn main() {
// Define a struct that will be our circuit. This struct will implement the FCircuit trait.
#[derive(Clone, Copy, Debug)]
pub struct MultiInputsFCircuit<F: PrimeField> {
    _f: PhantomData<F>,
}
impl<F: PrimeField> FCircuit<F> for MultiInputsFCircuit<F> {
    type Params = ();

    fn new(_params: Self::Params) -> Result<Self, Error> {
        Ok(Self { _f: PhantomData })
    }
    fn state_len(&self) -> usize {
        5 // since the circuit has 5 inputs
    }
    fn external_inputs_len(&self) -> usize {
        0
    }

    /// computes the next state values in place, assigning z_{i+1} into z_i, and computing the new
    /// z_{i+1}
    fn step_native(
        &self,
        _i: usize,
        z_i: Vec<F>,
        _external_inputs: Vec<F>,
    ) -> Result<Vec<F>, Error> {
        let a = z_i[0] + F::from(4_u32);
        let b = z_i[1] + F::from(40_u32);
        let c = z_i[2] * F::from(4_u32);
        let d = z_i[3] * F::from(40_u32);
        let e = z_i[4] + F::from(100_u32);

        Ok(vec![a, b, c, d, e])
    }

    /// generates the constraints for the step of F for the given z_i
    fn generate_step_constraints(
        &self,
        cs: ConstraintSystemRef<F>,
        _i: usize,
        z_i: Vec<FpVar<F>>,
        _external_inputs: Vec<FpVar<F>>,
    ) -> Result<Vec<FpVar<F>>, SynthesisError> {
        let four = FpVar::<F>::new_constant(cs.clone(), F::from(4u32))?;
        let forty = FpVar::<F>::new_constant(cs.clone(), F::from(40u32))?;
        let onehundred = FpVar::<F>::new_constant(cs.clone(), F::from(100u32))?;
        let a = z_i[0].clone() + four.clone();
        let b = z_i[1].clone() + forty.clone();
        let c = z_i[2].clone() * four;
        let d = z_i[3].clone() * forty;
        let e = z_i[4].clone() + onehundred;

        Ok(vec![a, b, c, d, e])
    }
}
}

Using external inputs

In this example we set the state to be the previous state together with an external input, and the new state is an array which contains the new state and a zero which will be ignored.

This is useful for example if we want to fold multiple verifications of signatures, where the circuit F checks the signature and is folded for each of the signatures and public keys. To keep things simpler, the following example does not verify signatures but does a similar approach with a chain of hashes, where each iteration hashes the previous step output ( $z_{i}$ ) together with an external input ( $w_{i}$ ).

       w_1     w_2     w_3     w_4     
       │       │       │       │      
       ▼       ▼       ▼       ▼      
      ┌─┐     ┌─┐     ┌─┐     ┌─┐     
─────►│F├────►│F├────►│F├────►│F├────►
 z_1  └─┘ z_2 └─┘ z_3 └─┘ z_4 └─┘ z_5


where each F is:
  w_i                                        
   │     ┌────────────────────┐              
   │     │FCircuit            │              
   │     │                    │              
   └────►│ h =Hash(z_i[0],w_i)│              
────────►│ │                  ├───────►      
 z_i     │ └──►z_{i+1}=[h]    │  z_{i+1}
         │                    │              
         └────────────────────┘

where each $w_{i}$ value is set at the external_inputs array.

The last state $z_{i}$ is used together with the external input w_i as inputs to compute the new state $z_{i + 1}$ .

#![allow(unused)]
fn main() {
use ark_crypto_primitives::{
    crh::{
        poseidon::constraints::{CRHGadget, CRHParametersVar},
        poseidon::CRH,
        CRHScheme, CRHSchemeGadget,
    },
    sponge::{poseidon::PoseidonConfig, Absorb},
};

#[derive(Clone, Debug)]
pub struct ExternalInputsCircuits<F: PrimeField>
where
    F: Absorb,
{
    _f: PhantomData<F>,
    poseidon_config: PoseidonConfig<F>,
}
impl<F: PrimeField> FCircuit<F> for ExternalInputsCircuit<F>
where
    F: Absorb,
{
    type Params = PoseidonConfig<F>;

    fn new(params: Self::Params) -> Result<Self, Error> {
        Ok(Self {
            _f: PhantomData,
            poseidon_config: params,
        })
    }
    fn state_len(&self) -> usize {
        1
    }
    fn external_inputs_len(&self) -> usize {
        1
    }

    /// computes the next state value for the step of F for the given z_i and external_inputs
    /// z_{i+1}
    fn step_native(
        &self,
        _i: usize,
        z_i: Vec<F>,
        external_inputs: Vec<F>,
    ) -> Result<Vec<F>, Error> {
        let hash_input: [F; 2] = [z_i[0], external_inputs[0]];
        let h = CRH::<F>::evaluate(&self.poseidon_config, hash_input).unwrap();
        Ok(vec![h])
    }

    /// generates the constraints and returns the next state value for the step of F for the given
    /// z_i and external_inputs
    fn generate_step_constraints(
        &self,
        cs: ConstraintSystemRef<F>,
        _i: usize,
        z_i: Vec<FpVar<F>>,
        external_inputs: Vec<FpVar<F>>,
    ) -> Result<Vec<FpVar<F>>, SynthesisError> {
        let crh_params =
            CRHParametersVar::<F>::new_constant(cs.clone(), self.poseidon_config.clone())?;
        let hash_input: [FpVar<F>; 2] = [z_i[0].clone(), external_inputs[0].clone()];
        let h = CRHGadget::<F>::evaluate(&crh_params, &hash_input)?;
        Ok(vec![h])
    }
}
}

Complete examples

You can find the complete examples with all the imports at sonobe/examples.

Circom frontend

Note: Circom frontend will be significantly slower than the Arkworks frontend. We explain below how to implement a custom step_native function with your circom circuits to speed things up!

Experimental frontend using arkworks/circom-compat.

We can define the circuit to be folded in Circom. The only interface that we need to fit in is:

template Example(ivc_state_len, aux_inputs_len) {
    signal input ivc_input[ivc_state_len]; // IVC state
    signal input external_inputs[aux_inputs_len]; // external inputs, not part of the folding state

    signal output ivc_output[ivc_state_len]; // next IVC state
    
    // here it goes the Circom circuit logic
}
component main {public [ivc_input]} = Example();

The ivc_input is the array that defines the initial state, and the ivc_output is the array that defines the output state after the step. Both need to be of the same size. The external_inputs array expects auxiliary input values.

In the following image, the ivc_input= $z_{i}$ , the external_inputs= $w_{i}$ , and the ivc_output= $z_{i + 1}$ , and $F$ is the logic of our Circom circuit:

So for example, the following circuit proves (at each folding step) knowledge of $x$ such that $y == x^{3} + e_{0} x + e_{1}$ for a known $y$ ( $e_{i}$ are the external_inputs[i]):

pragma circom 2.0.3;

template CubicCircuit() {
    signal input ivc_input[1]; // IVC state
    signal input external_inputs[2]; // not part of the state

    signal output ivc_output[1]; // next IVC state

    signal temp1;
    signal temp2;
    
    temp1 <== ivc_input[0] * ivc_input[0];
    temp2 <== ivc_input[0] * external_inputs[0];
    ivc_output[0] <== temp1 * ivc_input[0] + temp2 + external_inputs[1];
}

component main {public [ivc_input]} = CubicCircuit();

Once your circom circuit is ready, you can instantiate it with Sonobe. To do this, you will need the struct CircomFCircuit.

#![allow(unused)]
fn main() {
// we load our circom compiled R1CS, along with the witness wasm calculator
let r1cs_path = PathBuf::from("./src/frontend/circom/test_folder/cubic_circuit.r1cs");
let wasm_path =
    PathBuf::from("./src/frontend/circom/test_folder/cubic_circuit_js/cubic_circuit.wasm"); 
let f_circuit_params = (r1cs_path, wasm_path, 1, 2); // state_len:1, external_inputs_len:2
let f_circuit = CircomFCircuit::<Fr>::new(f_circuit_params).unwrap();


// [optional] to speed things up, you can define a custom step function to avoid
// defaulting to the snarkjs witness calculator for the native computations,
// which would be slower than rust native operations
circom_fcircuit.set_custom_step_native(Rc::new(|_i, z_i, _external| {
            let z = z_i[0];
            Ok(vec![z * z * z + z + Fr::from(5)])
        }));

pub type N =
    Nova<G1, GVar, G2, GVar2, CircomFCircuit<Fr>, KZG<'static, Bn254>, Pedersen<G2>, false>;
pub type D = DeciderEth<
    G1,
    GVar,
    G2,
    GVar2,
    CircomFCircuit<Fr>,
    KZG<'static, Bn254>,
    Pedersen<G2>,
    Groth16<Bn254>,
    N,
>;

let poseidon_config = poseidon_canonical_config::<Fr>();
let mut rng = rand::rngs::OsRng;

// prepare the Nova prover & verifier params
let nova_preprocess_params = PreprocessorParam::new(poseidon_config, f_circuit.clone());
let nova_params = N::preprocess(&mut rng, &nova_preprocess_params).unwrap();

// initialize the folding scheme engine, in this case we use Nova
let mut nova = N::init(&nova_params, f_circuit.clone(), z_0).unwrap();

// run n steps of the folding iteration
for (i, external_inputs_at_step) in external_inputs.iter().enumerate() {
    let start = Instant::now();
    // the last parameter at 'nova.prove_step()' is for schemes that support
    // folding more than 2 instances at each fold, such as HyperNova. Since
    // we're using Nova, we just set it to 'None'
    nova.prove_step(rng, external_inputs_at_step.clone(), None)
        .unwrap();
    println!("Nova::prove_step {}: {:?}", i, start.elapsed());
}

}

You can find a full example using Nova to fold a Circom circuit at sonobe/examples/circom_full_flow.rs.

Noir frontend

Experimental frontend using arkworks_backend.

If you write your R1CS circuits using Noir, you can also use sonobe to fold your circuits. Under the hood, we bridge compiled Noir circuits to arkworks R1CS. Beware that sonobe assumes that the compiled Noir circuit that is being folded does not use any other opcode than an arithmetic gate: you can not fold circuits calling oracles or using unconstrained functions. You should be able to use Noir's standard library though.

Using Noir with sonobe is similar to using any other frontend. Sonobe expects that the length of your public and private (external) inputs match what the Noir circuit expects. Note that sonobe does not expect your public inputs to follow some specific naming convention when using Noir: it will assume that whatever public input variable you have is the IVC state.

This example shows how to fold a poseidon circuit from the Noir standard library.

Noname frontend

Experimental frontend using ark-noname.

If you write your R1CS circuits using Noname, you can also use sonobe to fold your circuits. Under the hood, we bridge compiled Noname circuits to arkworks R1CS. Our Noname integration does not support Noname's standard library for now.

Using Noname with sonobe is similar to using any other frontend. Sonobe expects that the length of your public and private (external) inputs match what the Noname circuit expects. Note that sonobe does not expect your public inputs to follow some specific naming convention when using Noname: it will assume that whatever public input variable you have is the IVC state.

This example shows how to fold a simple Noname circuit having both public and external, private inputs.

Fold

We plug our FCircuit into the library:

#![allow(unused)]
fn main() {
// The idea here is that we could replace the next line chunk that defines the
// `type NOVA = Nova<...>` by using another folding scheme that fulfills the `FoldingScheme`
// trait, and the rest of our code would be working without needing to be updated.
type F = Nova<
    Projective,
    GVar,
    Projective2,
    GVar2,
    Sha256FCircuit<Fr>,
    KZG<'static, Bn254>,
    Pedersen<Projective2>,
    false,
>;

let num_steps = 10;
let initial_state = vec![Fr::from(1_u32)];

let F_circuit = Sha256FCircuit::<Fr>::new(());

let poseidon_config = poseidon_canonical_config::<Fr>();
let mut rng = rand::rngs::OsRng;

println!("Prepare Nova ProverParams & VerifierParams");
let nova_preprocess_params = PreprocessorParam::new(poseidon_config, F_circuit);
let nova_params = FS::preprocess(&mut rng, &nova_preprocess_params).unwrap();


println!("Initialize FoldingScheme");
let mut folding_scheme = FS::init(&nova_params, F_circuit, initial_state.clone()).unwrap();


// compute a step of the IVC
for i in 0..num_steps {
    let start = Instant::now();
    // - 2nd parameter: here we pass an empty vec since the FCircuit that we're
    // using does not use external_inputs
    // - 3rd parameter: is for schemes that support folding more than 2
    // instances at each fold, such as HyperNova. Since we're using Nova, we just
    // set it to 'None'
    folding_scheme.prove_step(rng, vec![], None).unwrap();
    println!("Nova::prove_step {}: {:?}", i, start.elapsed());
}

let (running_instance, incoming_instance, cyclefold_instance) = folding_scheme.instances();

println!("Run the Nova's IVC verifier");
FS::verify(
    nova_params.1,
    initial_state,
    folding_scheme.state(), // latest state
    Fr::from(num_steps as u32),
    running_instance,
    incoming_instance,
    cyclefold_instance,
)
.unwrap();
}

Now imagine that we want to switch the folding scheme being used. Is as simple as replacing FS by:

#![allow(unused)]
fn main() {
type FS = HyperNova<
    Projective,
    GVar,
    Projective2,
    GVar2,
    CubicFCircuit<Fr>,
    KZG<'static, Bn254>,
    Pedersen<Projective2>,
    1, 1, false,
>; 
}

and then adapting the folding_scheme.prove_step(...) call accordingly.

As in the previous sections, you can find a full examples with all the code at sonobe/examples.

Decider prove

Two options:

onchain (Ethereum's EVM) mode
offchain mode

Once we have been folding our circuit instances, we can generate the "final proof", the Decider proof.

Onchain Decider

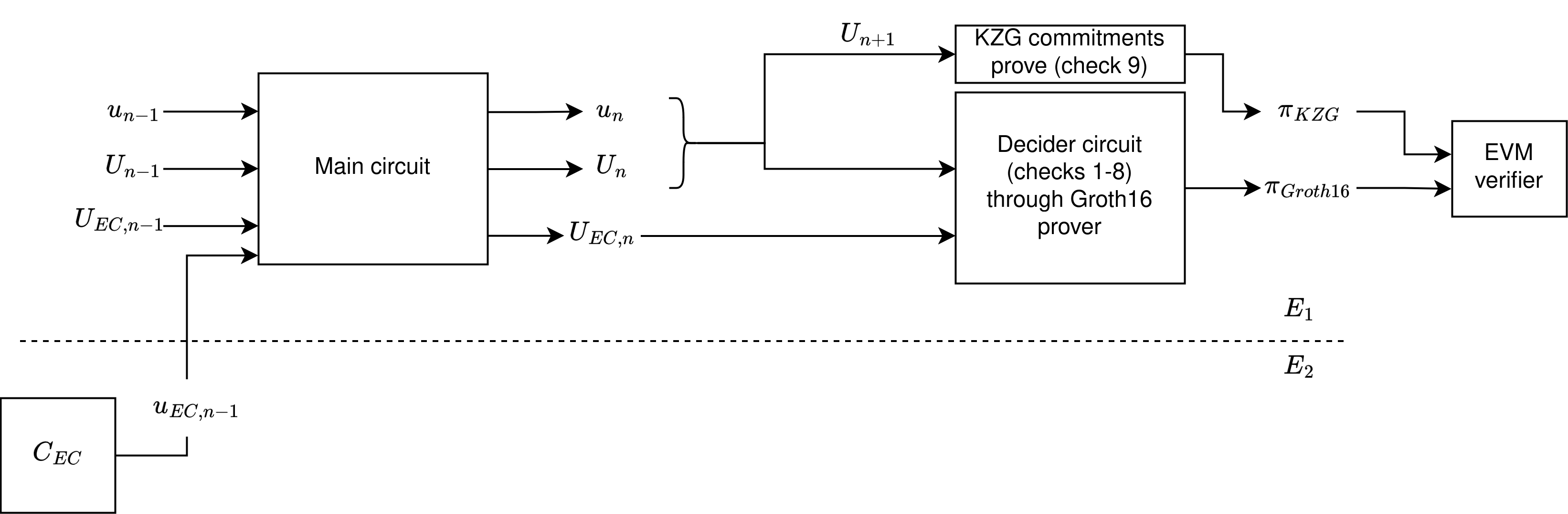
Generating the final proof (decider), to be able to verify it in Ethereum's EVM:

#![allow(unused)]
fn main() {
type DECIDER = Decider<
    Projective,
    GVar,
    Projective2,
    GVar2,
    CubicFCircuit<Fr>,
    KZG<'static, Bn254>,
    Pedersen<Projective2>,
    Groth16<Bn254>, // here we define the Snark to use in the decider
    NOVA,           // here we define the FoldingScheme to use
>;

let mut rng = rand::rngs::OsRng;

// prepare the Decider prover & verifier params for the given nova_params and nova instance. This involves generating the Groth16 and KZG10 setup
let (decider_pp, decider_vp) = DECIDER::preprocess(&mut rng, &nova_params, nova.clone()).unwrap();

// decider proof generation
let proof = DECIDER::prove(rng, decider_pp, nova.clone()).unwrap();

}

As in the previous sections, you can find a full examples with all the code at sonobe/examples.

Decider verify

We can now verify the Decider proof

#![allow(unused)]
fn main() {
// this is the same that we defined for the prover
type DECIDER = Decider<
    Projective,
    GVar,
    Projective2,
    GVar2,
    CubicFCircuit<Fr>,
    KZG<'static, Bn254>,
    Pedersen<Projective2>,
    Groth16<Bn254>,
    NOVA,
>;

let verified = DECIDER::verify(
    decider_vp, nova.i, nova.z_0, nova.z_i, &nova.U_i, &nova.u_i, proof,
)
.unwrap();
assert!(verified);
}

In the Ethereum Decider case, we can generate a Solidity smart contract that verifies the proofs onchain. More details in the next section.

Solidity verifier

Having used the Decider from decider_eth.rs, we can now verify it in Ethereum's EVM.

This can be done either by using the solidity-verifiers-cli or directly in rust code.

Using the CLI to generate the Solidity verifier

Use the solidity-verifiers-cli tool

> solidity-verifier-cli -p nova-cyclefold -d ./folding-verifier-solidity/assets/G16_test_vk_data

Generating the Solidity verifier in rust

Assuming that we already have our Decider initialized, we can now

#![allow(unused)]
fn main() {
// prepare the call data
let function_selector =
    get_function_selector_for_nova_cyclefold_verifier(nova.z_0.len() * 2 + 1);
let calldata: Vec<u8> = prepare_calldata(
    function_selector,
    nova.i,
    nova.z_0,
    nova.z_i,
    &nova.U_i,
    &nova.u_i,
    proof,
)
.unwrap();

// prepare the setup params for the solidity verifier
let nova_cyclefold_vk = NovaCycleFoldVerifierKey::from((decider_vp, f_circuit.state_len()));

// generate the solidity code
let decider_solidity_code = get_decider_template_for_cyclefold_decider(nova_cyclefold_vk);

// verify the proof against the solidity code in the EVM
let nova_cyclefold_verifier_bytecode = compile_solidity(&decider_solidity_code, "NovaDecider");
let mut evm = Evm::default();
let verifier_address = evm.create(nova_cyclefold_verifier_bytecode);
let (_, output) = evm.call(verifier_address, calldata.clone());
assert_eq!(*output.last().unwrap(), 1);

// save smart contract and the calldata
println!("storing nova-verifier.sol and the calldata into files");
use std::fs;
fs::write( "./examples/nova-verifier.sol", decider_solidity_code.clone()).unwrap();
fs::write("./examples/solidity-calldata.calldata", calldata.clone()).unwrap();
let s = solidity_verifiers::utils::get_formatted_calldata(calldata.clone());
fs::write("./examples/solidity-calldata.inputs", s.join(",\n")).expect("");
}

You can find the full flow at examples/full_flow.rs.

Nova's Zero-Knowledge Layer

Nova shows how to achieve zero-knowledge at the Decider level using an ad-hoc zk-SNARK (Spartan in the original Nova paper). This involves compressing and hiding a proof of knowledge of a valid IVC proof. Indeed, an IVC proof is not zero-knowledge by default: the prover must provide an IVC verifier with witness values to verify the correctness of their IVC computation.

The updated version of the HyperNova paper (section D.4), specifies a design for generating zk-IVC proofs which also applies to the Nova IVC. This allows an IVC prover to send an IVC verifier a zero-knowledge proof that hides the values attesting to the correctness of an IVC computation.

Use Cases

Nova's zk-IVC proof generation is quite efficient, as it simply involves blinding private field elements with randomly sampled values and folding the instances with randomized instances. It can be applied to a variety of use cases.

We identify 3 main interesting places to use the nova zk-layer: one before all the folding pipeline (Use-case-1), one at the end of the folding pipeline right before the final Decider SNARK proof (Use-case-2), and a third one for cases where compressed SNARK proofs are not needed, and just IVC proofs (bigger than SNARK proofs) suffice (Use-case-3):

Use-case-1: at the beginning of the folding pipeline, right when the user has their original instance prior to be folded into the running instance, the user can fold it with the random-satisfying-instance to then have a blinded instance that can be sent to a server that will fold it with the running instance.
- In this one, the user could externalize all the IVC folding and also the Decider final proof generation to a server.
Use-case-2: at the end of all the IVC folding steps (after n iterations of nova.prove_step), to 'blind' the IVC proof so then it can be sent to a server that will generate the final Decider SNARK proof.
- In this one, the user could externalize the Decider final proof generation to a server.
Use-case-3: the user does not care about the Decider (final compressed SNARK proof), and wants to generate a zk-proof of the last IVC state to an IVC verifier (without any SNARK proof involved). In this use-case, the zk is only added at the last IVCProof. Note that this proof will be much bigger and expensive to verify than a Decider SNARK proof.

The current implementation available in Sonobe covers the Use-case-3. Use-case-1 can be achieved directly by a simpler version of the zk IVC scheme skipping steps and implemented directly at the app level by folding the original instance with a randomized instance (steps 2,3,4 from section D.4 of the HyperNova paper). And the Use-case-2 would require a modified version of the Decider circuits.

Example (use case 3)

It is straightforward to obtain a zk IVC proof from the nova computation by:

#![allow(unused)]
fn main() {
// where `&nova` is of type `Nova<...>`
// returns a `Result`, containing a zk IVC nova proof if successful
let proof = RandomizedIVCProof::new(&nova, &mut rng);
}

See here for a small demo on how to generate and verify a zk IVC nova proof for the described use-case 3.

WASM - browser usage

WASM targets

In order to build the lib for WASM-targets, use the following command:

cargo build -p folding-schemes --no-default-features --target wasm32-unknown-unknown --features "parallel"

Where the target can be any WASM one and the parallel feature is optional.

WASM-compatibility & features

getrandom/js needs to be imported in the Cargo.toml of the crate that uses sonobe as dependency:

[dependencies]
folding-schemes = { git = "https://github.com/privacy-scaling-explorations/sonobe", package = "folding-schemes", default-features = false, features = ["parallel"] }
getrandom = { version = "0.2", features = ["js"] }

More details about getrandom.

Experimental frontends & WASM

Not all experimental frontends are supported in the browser.

Circom frontend & WASM

In order to use the Circom experimental browser, the feature circom-browser needs to be set.

Modularity

Swapping curves and proving schemes

Thanks to the modularity of arkworks, we can swap between curves and proving systems. Suppose that for the final proof (decider), instead of using Groth16 over the BN254 curve, we want to use Marlin+IPA over the Pasta curves, so we can enjoy of not needing a trusted setup. It just requires few line changes on our previous code [...]

Design

Notation

We work on a cycle of curves composed by $E_{1}$ and $E_{2}$ , where $E_{1} . F_{r} = E_{2} . F_{q}$ and $E_{1} . F_{q} = E_{2} . F_{r}$ . We will use $F_{r}$ to refer to $E_{1} . F_{r} = E_{2} . F_{q}$ , and $F_{q}$ to refer to $E_{1} . F_{q} = E_{2} . F_{r}$ . The main circuit constraint field is $F_{r}$ , and $C_{EC}$ circuit constraint field is $F_{q}$ (in some cases we use also $C^{*}$ , both notations come from papers).

Nova + CycleFold

CycleFold improves the usage of the cycle of curves proposed in Nova.

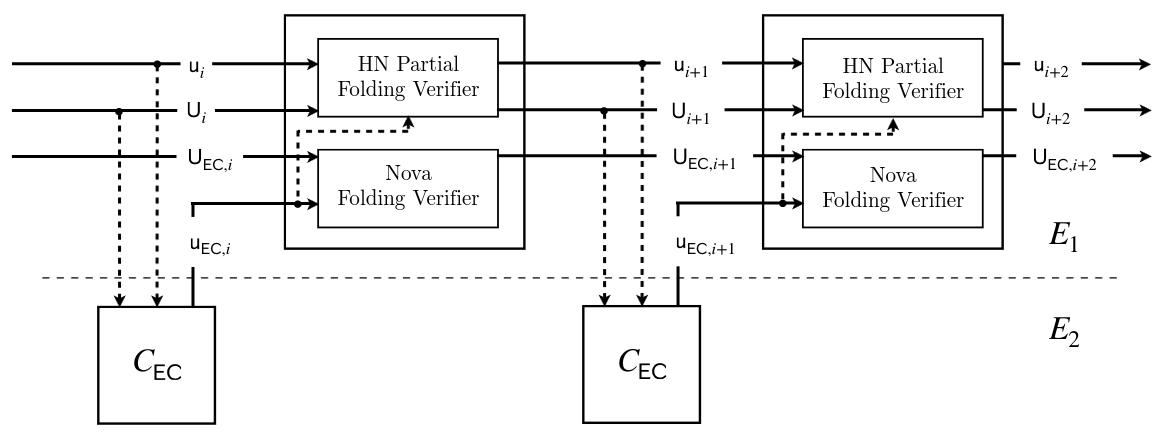CycleFold applied to HyperNova, src: https://eprint.iacr.org/2023/1192.pdf

We use a concrete version of the CycleFold approach applied to Nova.

The following image provides a description of the main Nova circuit and CycleFold circuit over a couple of steps, implemented at nova/circuits.rs and nova/cyclefold.rs.

Decider for Onchain Verification

Overview

This section describes the details of Sonobe's Decider, which is a zkSNARK that compresses the IVC's final proof.

Given an IVC scheme constructed with a folding scheme based on the CycleFold approach, the decider described in this section allows one to efficiently verify the final proof onchain in Ethereum's EVM.

Below we use Nova as a concrete example of the folding scheme, but the decider itself is generic and can be used with any other folding scheme.

Warning: This section, as the rest of Sonobe, is experimental. The approach described in this section is highly experimental and has not been audited.

Context

At the final stage of IVC based on Nova+CycleFold, after $n$ iterations, we have the committed instances ${u_{n}, U_{n}, U_{EC, n}}$ and their respective witnessess, where $u_{n}$ is the incoming instance, $U_{n}$ is the running instance, and $U_{EC, n}$ is the CycleFold (running) instance.

Diagram source: CycleFold paper (https://eprint.iacr.org/2023/1192.pdf). In the case of this document $n = i + 2$ , so $u_{i + 2} = u_{n}$ , $U_{i + 2} = U_{n}$ , $U_{EC, i + 2} = U_{EC, n}$ .

Since the objective is to verify the proofs on Ethereum, we set $E_{1}$ =BN254 and $E_{2}$ =Grumpkin. Thus, $F_{r}$ is the scalar field of the BN254.

The $u_{n}$ and $U_{n}$ contain: ${\overline{E} \in E_{1}, \overline{W} \in E_{1}, u \in F_{r}, x \in F_{r}^{∣ i o ∣}}$

And $U_{EC, n}$ contains: ${\overline{E} \in E_{2}, \overline{W} \in E_{2}, u \in F_{q}, x \in F_{q}^{∣ i o ∣}}$

Decider high level checks

Consider the Nova-based IVC for R1CS, where $r 1 cs$ is the R1CS for the augmented circuit AugmentedFCircuit, and $r 1 c s_{EC}$ is the R1CS for the CycleFold circuit CycleFoldCircuit.

The decider is essentially responsible for ensuring the validity of $I V C . V$ , which contains the following checks:

$R_{r 1 cs} (W_{n}, U_{n}) = 1$ :
- The running instance $U_{n}$ and witness $W_{n}$ satisfy (relaxed) $r 1 cs$ .
- The commitments in $U_{n}$ open to the values in $W_{n}$ .
$R_{r 1 cs} (w_{n}, u_{n}) = 1$ :
- The incoming instance $u_{n}$ and witness $w_{n}$ satisfy (plain) $r 1 cs$ .
- The commitments in $u_{n}$ open to the values in $w_{n}$ .
$R_{r 1 c s_{EC}} (W_{EC, n}, U_{EC, n})$ :
- The CycleFold instance $U_{EC, n}$ and witness $W_{EC, n}$ satisfy (relaxed) $r 1 c s_{EC}$ .
- The commitments in $U_{EC, n}$ open to the values in $W_{EC, n}$ .
$u_{n}$ is valid:
- $u_{n} . x$ contains the correct hash of the initial and final states.
- $u_{n}$ is indeed an incoming instance.

In Sonobe, the logic above is implemented in a zkSNARK circuit. To reduce circuit size, we ask the prover to fold $W_{n}, U_{n}$ and $w_{n}, u_{n}$ one more time, obtaining $W_{n + 1}, U_{n + 1}$ . Now, the circuit only needs to check:

$U_{n + 1}$ is the correct folding of $U_{n}, u_{n}$ , i.e., $N I FS . V (r, U_{n}, u_{n}, \overline{T}) = U_{n + 1}$ .
$R_{r 1 cs} (W_{n + 1}, U_{n + 1}) = 1$ :
- The running instance $U_{n + 1}$ and witness $W_{n + 1}$ satisfy (relaxed) $r 1 cs$ .
- The commitments in $U_{n + 1}$ (i.e., $U_{n + 1} . {\overline{E}, \overline{W}} \in E_{1}$ ) open to the values in $W_{n + 1}$ (i.e., $W_{n + 1} . {E, W}$ ).
$R_{r 1 c s_{EC}} (W_{EC, n}, U_{EC, n})$ :
- The CycleFold instance $U_{EC, n}$ and witness $W_{EC, n}$ satisfy (relaxed) $r 1 c s_{EC}$ .
- The commitments in $U_{EC, n}$ (i.e., $U_{EC, n} . {\overline{E}, \overline{W}} \in E_{2}$ ) open to the values in $W_{EC, n}$ (i.e., $W_{EC, n} . {E, W}$ ).
$u_{n}$ is valid:
- $u_{n} . x$ contains the correct hash of the initial and final states, i.e., $u_{n} . x_{0} = H (n, z_{0}, z_{n}, U_{n})$ and $u_{n} . x_{1} = H (U_{EC, n})$
- $u_{n}$ is indeed an incoming instance, i.e., $u_{n} . \overline{E} = 0$ and $u_{n} . u = 1$ .

Note: These are the same checks for both the Onchain & Offchain Deciders. The difference lays on how are performed.

Onchain Decider approach

The decider proof is computed once, and after all the folding has taken place. Our aim is to be able to verify this proof in the Ethereum's EVM.

The prover computes $(U_{n + 1}, W_{n + 1}, \overline{T}) = N I FS . P ((U_{n}, W_{n}), (u_{n}, w_{n}))$

The Decider Circuit verifies in its R1CS relation over $F_{r}$ the checks described above. Below we explain how the checks are performed in the circuit (for circuit efficiency, the order of the checks is different from the one described above):

1: Enforce $U_{n + 1}$ and $W_{n + 1}$ satisfy $r 1 cs$ , the RelaxedR1CS relation of the AugmentedFCircuit
2: Check that $u_{n} . \overline{E} = 0$ and $u_{n} . u = 1$
3: Check that $u_{n} . x_{0} = H (n, z_{0}, z_{n}, U_{n})$ and $u_{n} . x_{1} = H (U_{EC, n})$
4: Commitments verification of $U_{EC, n} . {\overline{E}, \overline{W}}$ with respect to $W_{EC, n} . {E, W}$ , where Pedersen commitments are used
- This check is native in $F_{r}$ because $U_{EC, n} . {\overline{E}, \overline{W}} \in E_{2}$ .
5: Enforce $U_{EC, n}$ and $W_{EC, n}$ satisfy $r 1 c s_{EC}$ , the RelaxedR1CS relation of the CycleFoldCircuit
- This check involves non-native operations because $W_{EC, n} . {E, W} \in F_{q}$ . With naive sparse matrix-vector product, it blows up the number of constraints.
6.1: Partially enforce that $U_{n + 1}$ is the correct folding of $U_{n}, u_{n}$
- By partially, we mean that only field elements in $U_{n + 1}$ are checked, while the group elements (i.e., commitments) are not, as they are in $E_{1}$ and are expensive non-native operations.
7.1: Check correct computation of the KZG challenges $c_{E} = H (\overline{E} . {x, y}), c_{W} = H (\overline{W} . {x, y})$ which we do through in-circuit Transcript.
7.2: Check that the KZG evaluations are correct
- $e v a l_{W} == p_{W} (c_{W})$
- $e v a l_{E} == p_{E} (c_{E})$
  where $p_{W}, p_{E} \in F [X]$ are the interpolated polynomials from $W_{i + 1} . W, W_{i + 1} . E$ respectively.
  ie. $p_{W} (x) = in t er p o l a t e (W_{i + 1} . W, 0)$ , where $0$ is zero-padding to the next power of 2 length, and $in t er p o l a t e ()$ interpolates a (unique) polynomial from the vector

The rest of the checks are performed outside of the circuit by the verifier. In addition to verifying the decider proof, the verifier would have to check:

6.2: The commitments in $U_{n + 1}$ are the correct folding of those in $U_{n}, u_{n}$ , i.e., $U_{n + 1} . \overline{E} = U_{n} . \overline{E} + r \cdot \overline{T}$ and $U_{n + 1} . \overline{W} = U_{n} . \overline{W} + r \cdot u_{n} . \overline{W}$ .
- 6.1 and 6.2 in together enforce $N I FS . V (r, U_{n}, u_{n}, \overline{T}) = U_{n + 1}$ .
7.3: The KZG proofs are valid with respect to the commitments $U_{n + 1} . {\overline{E}, \overline{W}}$ and the challenges $c_{E}, c_{W}$ .
- 7.1, 7.2, and 7.3 together enforce that $W_{n + 1} . {E, W}$ are the openings to the commitments $U_{n + 1} . {\overline{E}, \overline{W}}$ .

If we use Pedersen commitment as the commitment scheme for generating $U_{n + 1}$ , the checks for commitments would be too expensive as they are non-native in-circuit. By changing the commitment scheme to KZG, we can separate the commitments verification into 7.1, 7.2, and 7.3, where 7.1 and 7.2 can be (relatively) cheaply verified in-circuit, and 7.3 can be verified outside of the circuit (onchain).

The prover would generate a Groth16 proof over BN254 for this Decider Circuit, which can later be verified onchain in the EVM together with the KZG commitments of check 7.1 and check 7.2.

In this way, the final proof to be verified onchain would be:

a Groth16 proof of the checks 1, 2, 3, 4, 5, 6.1, 7.1, 7.2
the KZG proofs verification (check 7.3)
the NIFS.V (check 6.2), which relates the inputs of the checks in the Groth16 proof and check 6.1

The RelaxedR1CS checker circuit

The "correct RelaxedR1CS relation" (used in check 1) is checked by the gadget proposed by Nalin Bhardwaj, which is a R1CS circuit that checks the RelaxedR1CS relation, more details here.

The idea is that we check in a R1CS circiut the RelaxedR1CS relation ( $A z \circ B z - u C z - E = 0$ ). Note that this approach has a blowup of 3x with respect to the original circuit number of constraints x (when using sparse representation of the matrices).

Circuit costs

Note: the number of constraints written in this section is the current values that we have, which we aim to reduce in future iterations.

Estimated costs of the full decider-onchain circuit:

(x is the number of constraints of the circuit that we're folding, and the AugmentedFCircuit takes ~52k constraints)

1: $U_{n + 1}$ relation: 3(x+52k)
2: $u_{n}$ check: <1000
3: $u_{n} . x$ hash check: 2634
4: Pedersen check of $U_{EC, n}$ commitments (native): <5M both commitments (including the inputs allocations). This is a couple of native MSMs of <1500 elements each one
5: $U_{EC, n}$ relation (non-native): 5.1M
6.1: Partial check of $N I FS . V$ : (cheap)
7.1: Check correct computation of the KZG challenges: 7708
7.2: Check that the KZG evaluations are correct 262k

Total: 3*(x+52_252) + 1000 + 2634 + 4_967_155 + 5_146_236 + 7708 + 262_000

eg: for a circuit of 500k constraints the decider circuit would take approximately 11.9M constraints.

As can be seen, most of the costs come from the Pedersen commitments verification and the $U_{EC, n}$ relation (checks 4 and 5 respectively).

decider for offchain verification

Overview: This section describes the Decider (compressed SNARK / final proof) for the non-ethereum use cases in which the verification of the Nova+CycleFold proofs is done offchain. For onchain Ethereum use cases, check out the decider-onchain section.

Setup

At the final stage of the Nova+CycleFold folding, after $d$ iterations, we have the committed instances ${u_{d}, U_{d}, U_{EC, d}}$ and their respective witnessess.

cyclefold diagram Diagram source: CycleFold paper (https://eprint.iacr.org/2023/1192.pdf). In the case of this document $d = i + 2$ , so $u_{i + 2} = u_{d}$ , $U_{i + 2} = U_{d}$ , $U_{EC, i + 2} = U_{EC, d}$ .

We work with a cycle of curves $E_{1}$ and $E_{2}$ , where $E_{1} . F_{r} = E_{2} . F_{q}$ and $E_{1} . F_{q} = E_{2} . F_{r}$ . We will use $F_{r}$ for referring to $E_{1} . F_{r} = E_{2} . F_{q}$ , and $F_{q}$ for referring to $E_{1} . F_{q} = E_{2} . F_{r}$ . The main circuit constraint field is $F_{r}$ , and $C_{EC}$ circuit constraint field is $F_{q}$ .

The $u_{d}$ and $U_{d}$ contain: ${\overline{E} \in E_{1}, \overline{W} \in E_{1}, u \in F_{r}, x \in F_{r}}$

And $U_{EC, d}$ contains: ${\overline{E} \in E_{2}, \overline{W} \in E_{2}, u \in F_{q}, x \in F_{q}^{n}}$

Decider high level checks

$U_{n + 1}$ is the correct folding of $U_{n}, u_{n}$ , i.e., $N I FS . V (r, U_{n}, u_{n}, \overline{T}) = U_{n + 1}$ .
$R_{r 1 cs} (W_{n + 1}, U_{n + 1}) = 1$ :
- The running instance $U_{n + 1}$ and witness $W_{n + 1}$ satisfy (relaxed) $r 1 cs$ .
- The commitments in $U_{n + 1}$ (i.e., $U_{n + 1} . {\overline{E}, \overline{W}} \in E_{1}$ ) open to the values in $W_{n + 1}$ (i.e., $W_{n + 1} . {E, W}$ ).
$R_{r 1 c s_{EC}} (W_{EC, n}, U_{EC, n})$ :
- The CycleFold instance $U_{EC, n}$ and witness $W_{EC, n}$ satisfy (relaxed) $r 1 c s_{EC}$ .
- The commitments in $U_{EC, n}$ (i.e., $U_{EC, n} . {\overline{E}, \overline{W}} \in E_{2}$ ) open to the values in $W_{EC, n}$ (i.e., $W_{EC, n} . {E, W}$ ).
$u_{n}$ is valid:
- $u_{n} . x$ contains the correct hash of the initial and final states, i.e., $u_{n} . x_{0} = H (n, z_{0}, z_{n}, U_{n})$ and $u_{n} . x_{1} = H (U_{EC, n})$
- $u_{n}$ is indeed an incoming instance, i.e., $u_{n} . \overline{E} = 0$ and $u_{n} . u = 1$ .

Note: These are the same checks for both the Onchain & Offchain Deciders. The difference lays on how are performed.

Offchain Decider approach

In the offchain case, since we can end up with proofs in both curves of the cycle, we try to fit all the computations natively in each curve respectively.

We use the same checks numbers as the ones used in the Onchain Decider in order to make the relation of the checks easier to follow.

Circuit1 $\in F r$ ( $E_{1} . F_{r}$ )

1: Enforce $U_{n + 1}$ and $W_{n + 1}$ satisfy $r 1 cs$ , the RelaxedR1CS relation of the AugmentedFCircuit
2: Check that $u_{n} . \overline{E} = 0$ and $u_{n} . u = 1$
3: Check that $u_{n} . x_{0} = H (n, z_{0}, z_{n}, U_{n})$ and $u_{n} . x_{1} = H (U_{EC, n})$
6.1: Partially enforce that $U_{n + 1}$ is the correct folding of $U_{n}, u_{n}$
- By partially, we mean that only field elements in $U_{n + 1}$ are checked, while the group elements (i.e., commitments) are not, as they are in $E_{1}$ and are expensive non-native operations.
7.1: Check correct computation of the KZG challenges $c_{E} = H (\overline{E} . {x, y}), c_{W} = H (\overline{W} . {x, y})$ which we do through in-circuit Transcript.
7.2: Check that the KZG evaluations are correct
- $e v a l_{W} == p_{W} (c_{W})$
- $e v a l_{E} == p_{E} (c_{E})$
  where $p_{W}, p_{E} \in F [X]$ are the interpolated polynomials from $W_{i + 1} . W, W_{i + 1} . E$ respectively.
  ie. $p_{W} (x) = in t er p o l a t e (W_{i + 1} . W, 0)$ , where $0$ is zero-padding to the next power of 2 length, and $in t er p o l a t e ()$ interpolates a (unique) polynomial from the vector

Circuit2 $\in Fq$ ( $E_{2} . F_{r}$ )

Note that in onchain decider, step 4 (Pedersen commitments verification of $U_{EC, n} . {\overline{E}, \overline{W}}$ ) is checked in-circuit, necessitating ~5M constraints.

In the case of offchain decider, we aim to reduce the number of constraints for commitment verification for CycleFold instances. To this end, we apply the same approach as in step 7 of the onchain decider for checking commitments in primary instances. That is, we now use KZG commitments as well for the CycleFold instances, enabling us to separate expensive parts in commitments verification from the circuit.

Below are checks for the Circuit2:

4.1: Check correct computation of the KZG challenges for $U_{EC}$ $c_{E} = H (U_{EC} . \overline{E} . {x, y}), c_{W} = H (U_{EC} . \overline{W} . {x, y})$ which we do through in-circuit Transcript.
4.2: check that the KZG evaluations for $U_{EC}$ are correct
- $e v a l_{W} == p_{W} (c_{W})$
- $e v a l_{E} == p_{E} (c_{E})$
  where $p_{W}, p_{E} \in F [X]$ are the interpolated polynomials from $W_{i + 1} . W, W_{i + 1} . E$ respectively.
5: Enforce $U_{EC, n}$ and $W_{EC, n}$ satisfy $r 1 c s_{EC}$ , the RelaxedR1CS relation of the CycleFoldCircuit
- This check becomes native because the constraint system is now over $F_{q}$ .

Outside the circuits

6.2. Check the commitments in $U_{n + 1}$ are the correct folding of those in $U_{n}, u_{n}$
7.3: Verify the KZG proofs with respect to the commitments $U_{n + 1} . {\overline{E}, \overline{W}} \in E_{1}$ and the challenges $c_{E}, c_{W}$ .
4.3: Verify the KZG proofs with respect to the commitments $U_{EC, n} . {\overline{E}, \overline{W}} \in E_{2}$ and the challenges $c_{E}, c_{W}$ .

Proving scheme

We could use a SNARK adapted to RelaxedR1CS, but before that is ready we use a regular R1CS SNARK and check the RelaxedR1CS relations in-circuit as described above. Two proofs are generated, one for each circuit over their respective curves of the cycle.

Examples and Projects

This section contains examples and projects that use Sonobe. You can find isolated examples too in the dir sonobe/examples.

sonobe-btc: implementation of an on-chain Bitcoin light client leveraging Sonobe: uses nova to verify bitcoin's proof of work over 100k blocks and groth16 to land the zkSNARK IVC proof on chain.
hash-chain-sonobe: example using Sonobe & Circom circuits, proving chains of Sha256 and Keccak256 hashes.

Papers

Mova: Nova folding without committing to error terms: a folding scheme for R1CS instances that does not require committing to error or cross terms. It is implemented on top of Sonobe code base, and used for benchmarks, see their repo here.
Eva: Efficient IVC-Based Authentication of Lossy-Encoded Videos: cryptographic protocol for authenticating lossy-encoded videos. Is implemented on top of Sonobe code base.

sonobe docs